
El teorema de Torricelli o principio de Torricelli es una aplicación del principio de Bernoulli y estudia
el flujo de un líquido contenido en un recipiente, a través de un pequeño orificio, bajo la acción de la gravedad. Fue propuesto por el físico matemático italiano Evangelista
Torricelli
A
partir del teorema de Torricelli se puede calcular el caudal de salida de un
líquido por un orificio.
Matemáticamente:
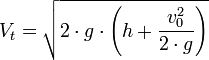
Donde:
· 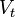 es la
velocidad teórica del líquido a la salida del orificio
es la
velocidad teórica del líquido a la salida del orificio
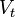 es la
velocidad teórica del líquido a la salida del orificio
es la
velocidad teórica del líquido a la salida del orificio
· 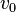 es la
velocidad de aproximación o inicial.
es la
velocidad de aproximación o inicial.
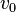 es la
velocidad de aproximación o inicial.
es la
velocidad de aproximación o inicial.
· 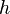 es la distancia desde la
superficie del líquido al centro del orificio.
es la distancia desde la
superficie del líquido al centro del orificio.
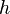 es la distancia desde la
superficie del líquido al centro del orificio.
es la distancia desde la
superficie del líquido al centro del orificio.
· 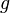 es la aceleración de la
gravedad.
es la aceleración de la
gravedad.
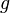 es la aceleración de la
gravedad.
es la aceleración de la
gravedad.
Para velocidades de aproximación
bajas, la mayoría de los casos, la expresión anterior se transforma en:

Dónde:
· 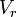 es la
velocidad real media del líquido a la salida del orificio
es la
velocidad real media del líquido a la salida del orificio
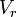 es la
velocidad real media del líquido a la salida del orificio
es la
velocidad real media del líquido a la salida del orificio
·  es el
coeficiente de velocidad. Para cálculos preliminares en aberturas de pared
delgada puede admitirse 0,95 en el caso más desfavorable.
es el
coeficiente de velocidad. Para cálculos preliminares en aberturas de pared
delgada puede admitirse 0,95 en el caso más desfavorable.
 es el
coeficiente de velocidad. Para cálculos preliminares en aberturas de pared
delgada puede admitirse 0,95 en el caso más desfavorable.
es el
coeficiente de velocidad. Para cálculos preliminares en aberturas de pared
delgada puede admitirse 0,95 en el caso más desfavorable.
Tomando  =1
=1
 =1
=1
Ejemplo de aplicación del
teorema de Torricelli (vaciado de un recipiente):
Un depósito cilíndrico, de sección S1 tiene un orificio muy pequeño en el fondo
de sección S2 mucho más pequeña que S1 :
Aplicamos el
teorema de Bernoulli suponiendo que la velocidad del fluido en la sección mayor.

Aplicamos el teorema
de Bernoulli suponiendo que la velocidad del fluido en la sección s1 es
despreciable, v1 es más o menos 0 comparada con la velocidad del fluido v2 en
la sección menor s2.
Por otra parte, el
elemento de fluido delimitado por las secciones S1 y S2 está en contacto
con el aire a la misma presión, luego p1=p2=p0.
Finalmente, la
diferencia entre alturas y1- y2 = H. siendo H la altura de la columna del fluido.
La ecuación de Bernoulli:
Con los datos del
problema se escribirá de una forma más simple:


No hay comentarios:
Publicar un comentario